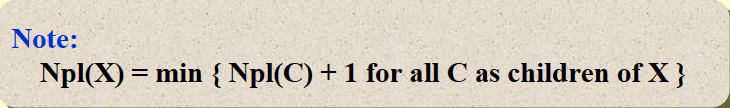跳转至

4. Leftist Heap & Skew Heap

约 5339 个字 166 行代码 预计阅读时间 29 分钟

什么是堆heap？

满足以下性质：

  1. 结构性质：堆是一棵完全二叉树。并且由于是完全二叉树，故树高h 和总结点数之间的关系显然为\(h = O(log n)\)。
  2. 序性质：对于最大堆，根结点就是最大元素，每一个结点的孩子都必须小于等于本身。反之对于最小堆，根结点是最大元素，孩子应当大于等于父亲。

基于数组的二叉堆实现，事实上是利用数组构造了一棵完全二叉树，我们可以通过数组索引除以2 找到结点的父亲，乘以2 和乘以2 加1 获得结点的左右孩子，因此非常方便，相比于指针需要寻址，这样的实现显然更加高效。

堆(最小堆)的基本操作：

  1. Insert : 直接插在完全二叉树的下一个空位上，然后percolate up 找到它应当在的位置，显然最坏情况也与完全二叉树的高度成正比，即\(O(log n)\)。
  2. FindMin : 直接返回根结点， \(O(1)\)
  3. DeleteMin： 直接用完全二叉树的最后一个元素顶替根结点，然后percolate down 找到新根结点的归宿，时间\(O(log n)\)
  4. BuildHeap: 对n 个元素建堆存储。
  5. 方法一：连续插入n次，但这样时间复杂度为\(O(n log n)\)
  6. 方法二：无需管序性质，直接任意插入这n 个值，然后从完全二叉树倒数第二排有孩子的结点开始，往前依次检查是否有违反序性质的，有就percolate down 到正确的位置，循环直到根结点也调整完毕为止，可以验证这样的算法复杂度为\(O(n)\)

在基于数组的实现中我们能想到的最好的方法也只能是直接合并两个数组，然后调用BuildHeap 在O(n) 时间内完成。

4.1 Leftist Heap

4.1.1 概念

左偏堆，或者说左偏堆(Leftist Heap)，它相比于普通的堆，更好的一点在于它支持快速的堆合并操作(speed up merging in O(N))。

“左偏”，并不断将新的东西往右侧合并，来实现每次都是往相对小的那一侧塞进东西，进而保相对证了这个

由于左偏堆不再是一个完全二叉树，所以我们不能再像维护大根堆小根堆那样用数组来维护它了。

// struct LeftistHeapNode {
    // ElementType val;
    // int Npl;
    // LeftistHeapNode * ls, * rs;
// };
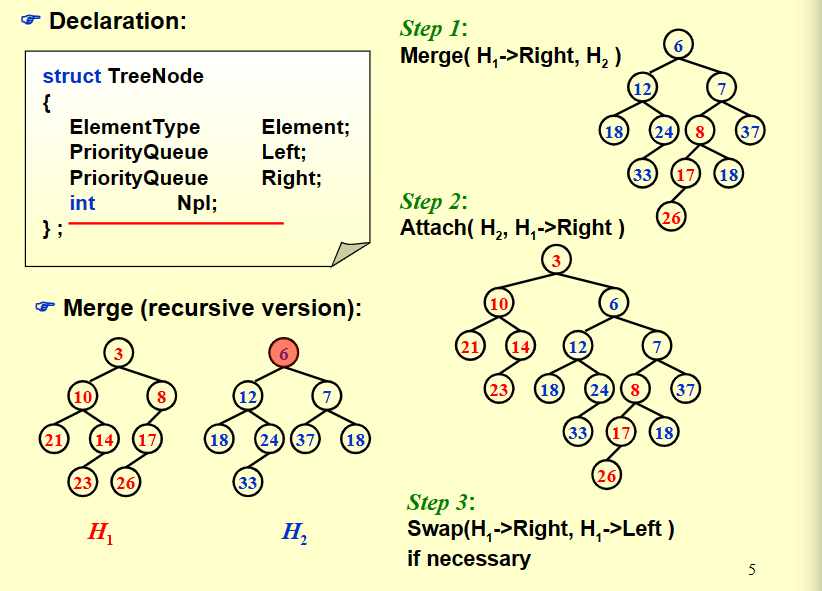
struct TreeNode
{
    ElementType     val;
    PriorityQueue   Left;
    PriorityQueue   Right;
    int             Npl;
};

definition “Npl” in leftist heap"

The null path length , Npl(X), of any node X is the length of the shortest path from X to a node without two children.

Npl(x) 表示从x开始到没有孩子结点的结点（可能是x本身）的最短路径的长度

Define Npl(NULL) = –1.

image-20240318101709749

  1. 如果一个结点的左孩子或右孩子为空结点，则该结点的 Npl 为 \(0\)，这种结点被称为外结点；
  2. 如果一个结点的左孩子和右孩子都不为空，则该结点的 Npl 为 \(\min{(npl_\text{left child}, npl_\text{right child})} + 1\)；

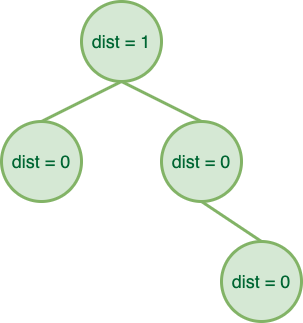
而左偏堆就建立在这些性质上：

definition "Leftist Heap"

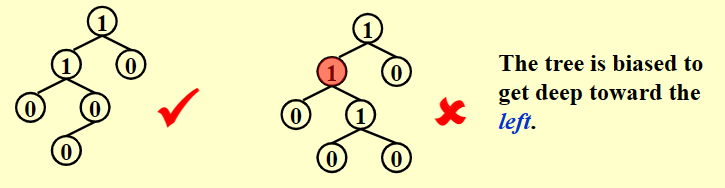
​ 左偏堆的性质

  1. 结点的value应当不大于（不小于）其孩子结点的value的二叉树（即堆的性质）
  2. 且满足「左偏」性质——结点的左孩子的 Npl 不小于右孩子的 Npl。

image-20240318102018200

虽然局部存在右子树结点数大于左子树，但是可能依然不影响左倾堆的性质

因此，回顾 Npl 的定义，我们可以得到扩展性质：

  1. A leftist tree with r nodes on the right path must have at least \(2^r -1\) nodes

在右路径上有r 个结点的左式堆必然至少有2r −1 个结点（右路径指从根结点出发一路找右孩子直到找到叶子的路径）。

证明： 使用数学归纳法进行证明

  • 若\(r = 1\),显然存在至少一个结点

  • 假设定理对右路径上小于等于\(r\)个结点的情况都成立。现在考虑在右路径上有\(r+1\)个结点的左倾堆。

    • 根的右子树恰好在右路径上有\(r\)个结点，因此右子树至少有\(2^r - 1\)个结点
    • 再考虑左子树。左倾堆的性质，左子树的\(Npl\)必须大于等于右子树的\(Npl\)，而右子树的\(Npl\)为\(n-1\),那么左子树结点到叶结点的距离至少为\(n-1\)
    • 利用子树也有左倾的性质，右路径\(Npl\)更短，所以右路径至少有\(r\)个结点，因此左子树的大小也为\(2^r -1\)
    • 所以整棵树的结点数至少为\(1 + 2^r-1 + 2^r -1 = 2 ^ {r+1} -1\)

根据性质1，可以得到共有N个结点的左倾堆的右路径最多含有log（N+1）个结点。

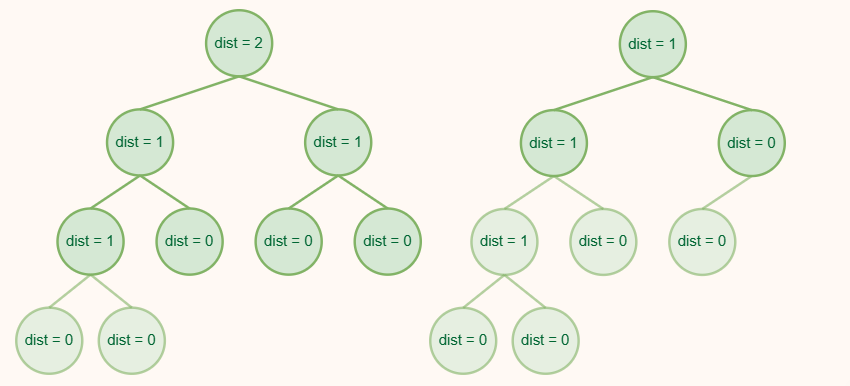
image-20240318102513008

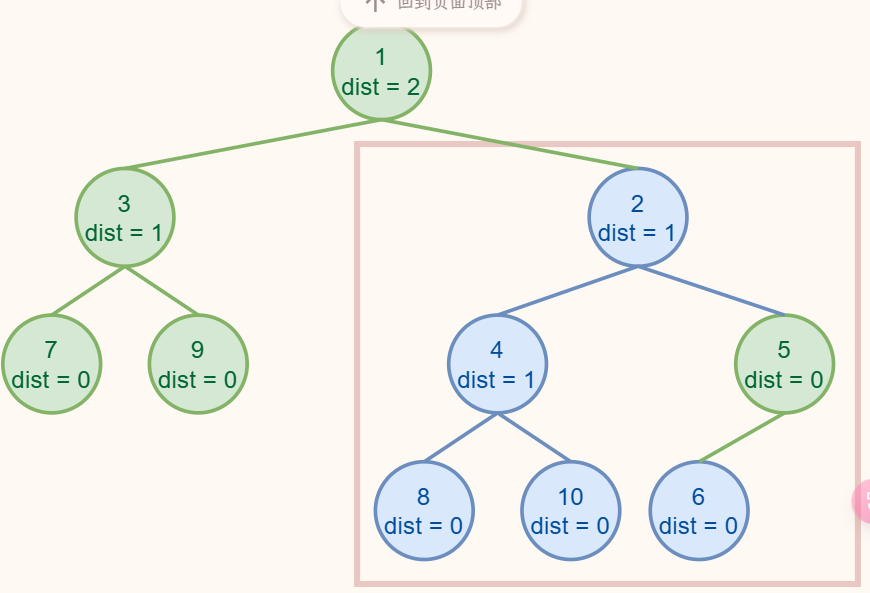
注意，在示意图中我们省略了结点自身键值的标记，但既然作为一个堆，它就需要满足堆的性质，即结点的键值不大于（不小于）其孩子结点的键值。在实际使用过程中，键值很可能不再是单纯的数，大小关系可能转化为偏序关系。

简单思考一下，为什么左偏堆会这么设计呢？实际上，合并堆需要考虑的非常重要的一个点就是要能在之后的操作中尽可能地维护堆的“平衡”，否则我们把堆维护成了一个链，那显然是非常糟糕的。

而左偏堆通过维护整个堆“左偏”，并不断往右侧合并，来实现每次都是往\(Npl\)相对小的那一侧塞进东西，进而保证了这个堆的相对平衡性。

4.1.2 Merge

左偏堆的核心操作就是合并。而其它操作都可以看作是合并的特殊情况。

  • Insert： 可以看作一个堆和一个单结点的堆的Merge
  • Delete Min：首先删除根结点，然后将根结点的两个子树进行Merge即可

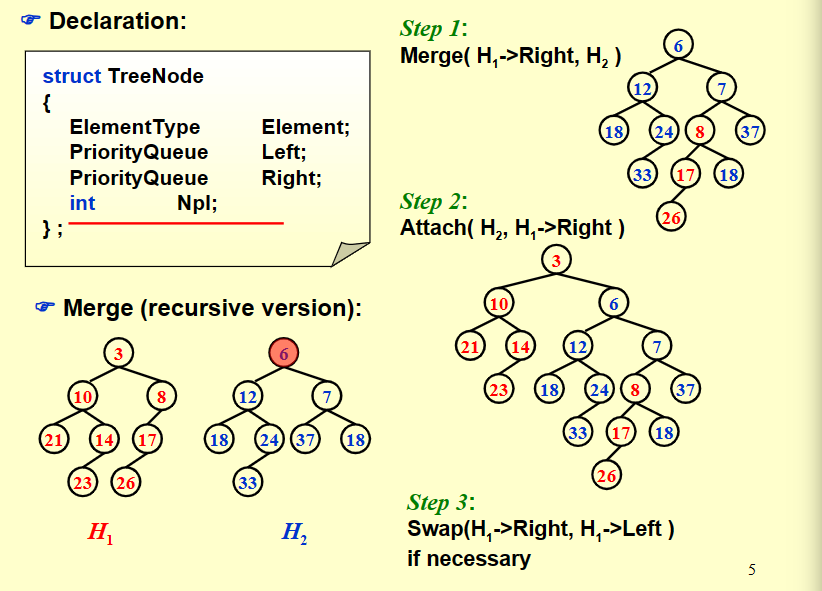
作为左偏堆的核心操作，合并操作自然就是要在满足性质的条件下，合并两个左偏堆。大致思路就是先维护堆的性质，在回溯时维护左偏性质，所以实际上它是一个先自上而下再自下而上的过程。

按照实现方法，左偏堆的合并可以分为递归式和迭代式两种。

image-20240318103735273

顶小的树记为H1，顶大的树记为H2

4.1.2.1 递归式

PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2)
{
    if (H1 == NULL && H2 == NULL)
        return NULL;
    else if (H1 && H2 == NULL)
        return H1;
    else if (H2 && H1 == NULL)
        return H2;
    else
    {
        if (H1->value < H2->value)
            return Merge1(H1, H2);
        else
            return Merge1(H2, H1);
    }
}
PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2)
{
    // Merge1 已将排除H1，H2为空的情况
    // 目前 H1的value小于H2的value
    if (H1->Left == NULL)
    {
        H1->Left = H2;
    }
    else
    {
        H1->Right = Merge(H1->Right, H2);
        if (H1->Left->Npl < H1->Right->Npl)
        {
            PriorityQueue temp = H1->Left;
            H1->Left = H1->Right;
            H1->Right = temp;
        }
    }
    if (!H1->Left || !H1->Right)
        H1->Npl = 0;
    else
        H1->Npl = H1->Right->Npl + 1;
    return H1;
}


PriorityQueue Merge_Recursive(PriorityQueue H1, PriorityQueue H2)
{
    if (H1 == NULL && H2 == NULL)
        return NULL;
    else if (H1 && H2 == NULL)
        return H1;
    else if (H2 && H1 == NULL)
        return H2;
    else
    {
        if(H1->value < H2->value)
        {
            if(!H1->Left)
            {
                H1->Left = H2;
            }
            else
            {
                H1->Right = Merge_Recursive(H1->Right, H2);
                if (H1->Left->Npl < H1->Right->Npl)
                {
                    PriorityQueue temp = H1->Left;
                    H1->Left = H1->Right;
                    H1->Right = temp;
                }
            }
            if (!H1->Left || !H1->Right)
                H1->Npl = 0;
            else
                H1->Npl = H1->Right->Npl + 1;
            return H1;
        }
        else
        {
            if(!H2->Left)
            {
                H2->Left = H1;
            }
            else
            {
                H2->Right = Merge_Recursive(H2->Right, H1);
                if (H2->Left->Npl < H2->Right->Npl)
                {
                    PriorityQueue temp = H2->Left;
                    H2->Left = H2->Right;
                    H2->Right = temp;
                }
            }
            if (!H2->Left || !H2->Right)
                H2->Npl = 0;
            else
                H2->Npl = H2->Right->Npl + 1;
            return H2;
        }
    }
}
  1. 如果两个堆中至少有一个为空，直接返回另一个即可
  2. 如果两个堆都非空，我们比较两个堆的根结点value的大小，value小的是\(H1\),value大的是\(H2\)
  3. 如果H1只有一个顶点（根据左倾堆的定义，只要没有左孩子，就一定只有一个根结点），直接把H2放在H1的左子树即可
  4. 如果H1不只有一个根结点，则将H1的右子树和H2merge（此处是递归，只要basecase正确，便能得到正确的结果），成为H1的新右子树
  5. 如果H1的Npl性质被违反，就交换两个子树
  6. 更新H1的Npl，结束任务

image-20240318103735273

image-20240319153752490

image-20240319153803164

another example:

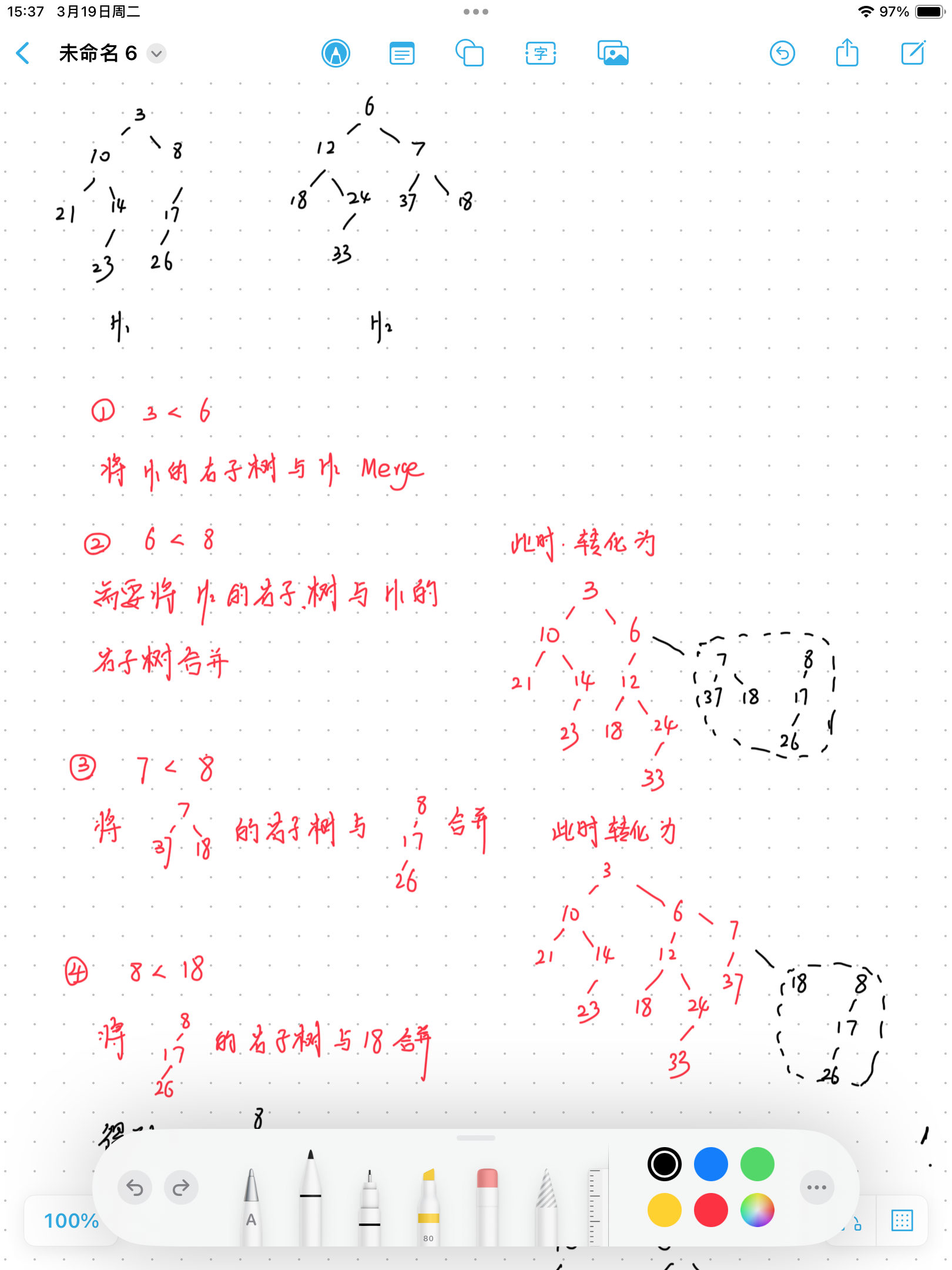
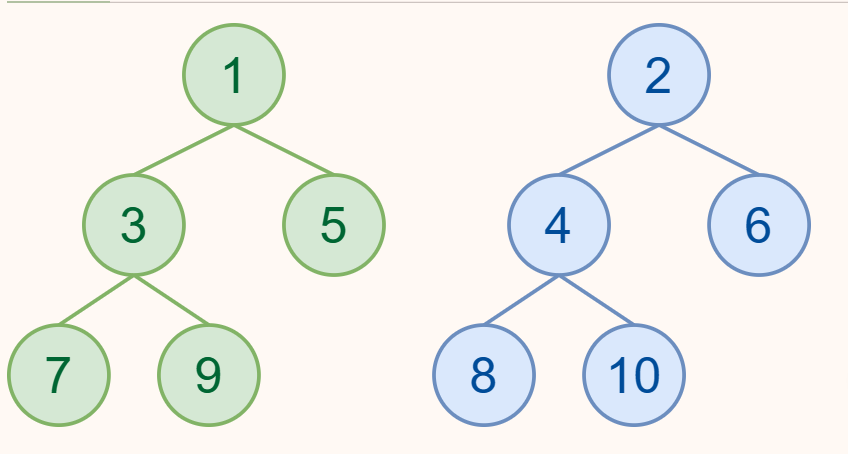
image-20240318105008505

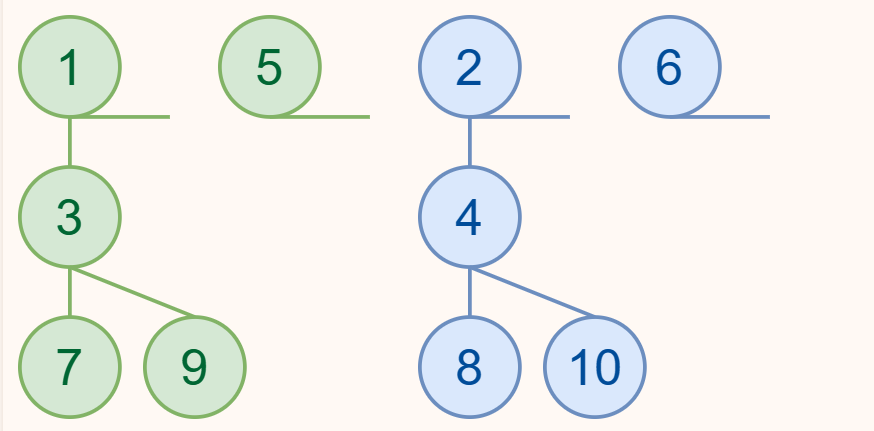
现在我们模拟一下这个过程，现在我们有下面两个左偏堆，尝试合并它们。

image-20240318105022021

我们发现，经过比较，❶ 更小，所以我们将 ❶ 作为合并后的根结点，左子树不变，右子树更新为「绿树右子树和蓝树的合并结果」。

image-20240318105037237

经过比较，❷ 更小，所以我们将 ❷ 作为合并后的根结点，左子树不变，右子树更新为「蓝树右子树和绿树的合并结果」。

image-20240318105056401

最后还剩下两个结点啦！实际上这里直接模拟了两个步骤，首先是比较 ❺ 和 ❻，并选择了 ❺ 作为新根；接下来在递归的过程中发现需要合并 NULL 和 ❻，所以直接返回了 ❻。

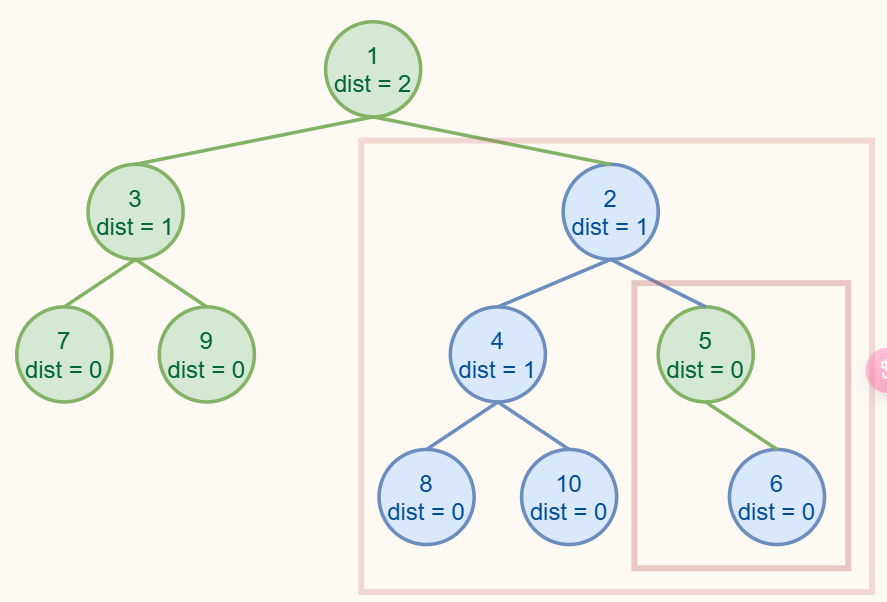
然而还没有结束，我们还需要处理左右子树 Npl 大小关系问题。

image-20240318105114614

我们发现 ❺ 的左孩子为 NULL，我们记 \(Npl_\text{NULL} = -1\)，右孩子 ❻ 有 \(Npl_\text{right child}=0\)，所以需要交换两个孩子。

image-20240318105132353

这里也跳过了两个步骤：

往回走，发现 ❺ 的 Npl 小于 ❹ 的 Npl，满足性质，不需要改变。

继续往回走，发现 ❷ 和 ❸ 的 Npl 相同，满足性质，也不需要改变。

从这里也可以看出来，并不是看上去更大的子树一定在左侧。

时间复杂度分析：

  1. 递归的最大深度是多少？我们发现，在递归过程中，产生的递归层数不会超过两个左倾堆右路径长度之和，因为每一次递归都会使两个堆其中之一（value更小的）向着右路径上下一个右孩子推进，知道其中一个推到了NULL结点。

  2. 加深一层的过程中，操作都是常数级别的，因为只需要比大小和找孩子

  3. 假设H1的结点总数为N1，H2的结点总数为N2，右路径小于等于log（N+1),所以两者右路径之和为 $$ O(logN_1 + logN_2) = O(logN_1N_2) = O(log\sqrt{N_1N_2} = O(log(N_1+N_2)) $$ 上面推导使用基本不等式\(a + b >= 2\sqrt{ab}\),两个堆右路径长度之和依然是两个堆大小的对数级别

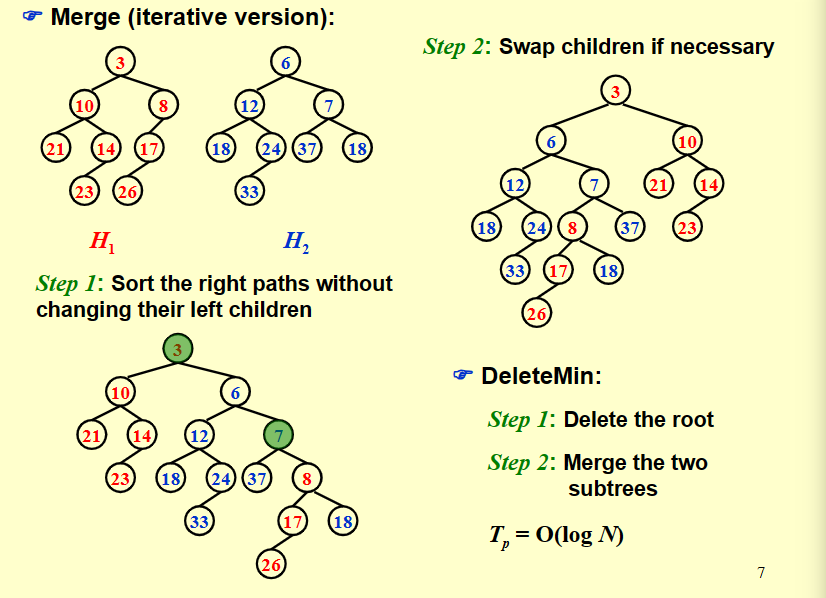
4.1.2.2迭代式

image-20240318105738215

3 -> 6 -> 7 -> 8 -> 18

上述递归的过程就等价于迭代的过程：每一次递归向下对应得带中保留根结点更小的堆的左子树，直到最后一次与NULL合并并直接接上。

递归返回的过程实际上就是逐个检查新的右路径上的结点是否有违反Npl性质，并且更新Npl。

在迭代法的运算中，在递归向下后，交换孩子调整左倾堆性质之前，合并后的堆的右路径就是原来两个堆的右路径合并排序的结果。因此，我们只需每次都在比较两个堆的右路径上的两个点的大小，将小的作为根结点插入。只需要把两条右路径从小到大排序，然后从小到大依次带着左子树接入到新的右路径即可（但要注意在此之后还需要调整使得满足左式堆结构性质）

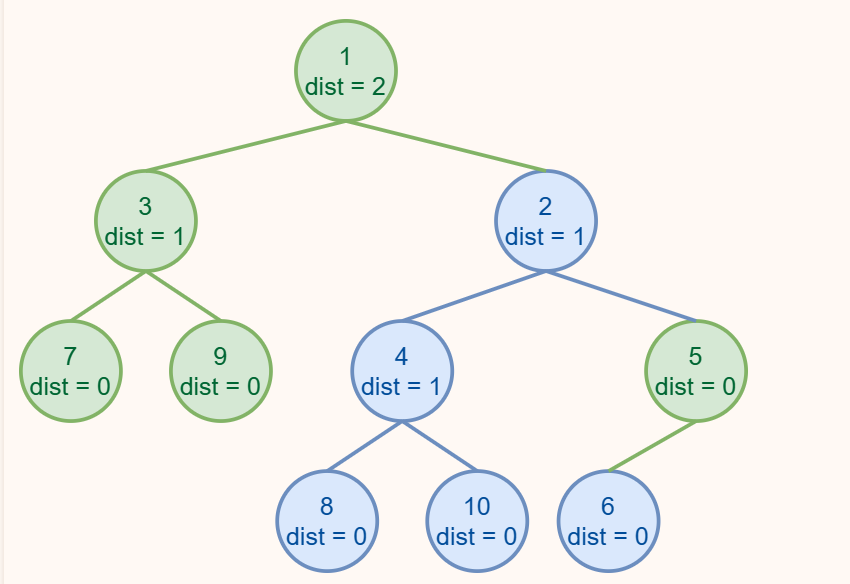
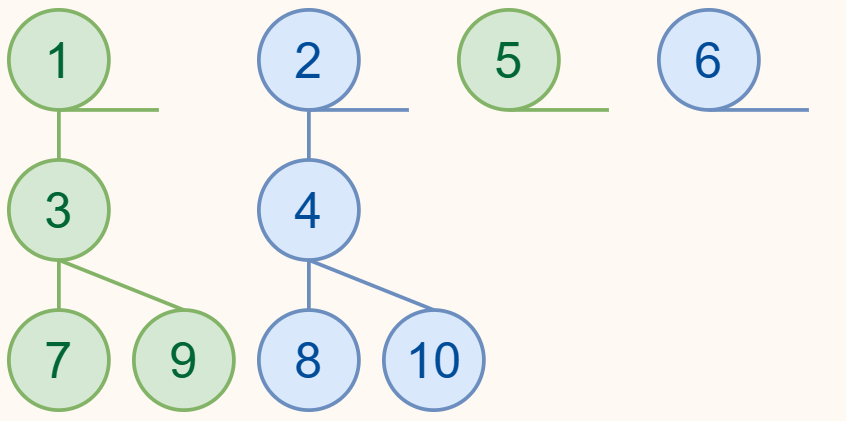
首先，我们对图片的排版稍微做一些改变，我们不再按照之前画堆的方式去画，而是“左偏”地去画：

img

可以发现，在调整之前

img

绿色和蓝色的箭头分别表示两个待合并子树尚未合并的子树的根，紫色箭头表示最近的合并发生的位置。

img

比较 ❶ 和 ❷，发现 ❶ 更小，所以我们将 ❶ 作为合并后的根结点，左子树随之合并进去，同时更新绿色箭头指向尚未合并进去的 ❺。

img

和上一步类似的，比较 ❺ 和 ❷，发现 ❷ 更小，所以我们将 ❷ 作为合并后的根结点，左子树随之合并进去，同时更新蓝色箭头指向尚未合并进去的 ❻。

img

依然类似地，比较 ❺ 和 ❻，发现 ❺ 更小，所以我们将 ❺ 作为合并后的根结点，左子树随之合并进去，同时更新绿色箭头指向 NULL。

img

这时候我们发现已经有一个指针空了，也就是绿色指针已经指向了 NULL，这个时候我们只需要按顺序把蓝色指针指向的内容都推进去即可。

img

接下来我们还需要维护 Npl 信息并根据性质交换左右子树。这一部分和之前一样，就不再赘述了。

在迭代法的运算中，在递归向下后，交换孩子调整左倾堆性质之前，合并后的堆的右路径就是原来两个堆的右路径合并排序的结果。因此，我们只需每次都在比较两个堆的右路径上的两个点的大小，将小的作为根结点插入。只需要把两条右路径从小到大排序，然后从小到大依次带着左子树接入到新的右路径即可（但要注意在此之后还需要调整使得满足左式堆结构性质）

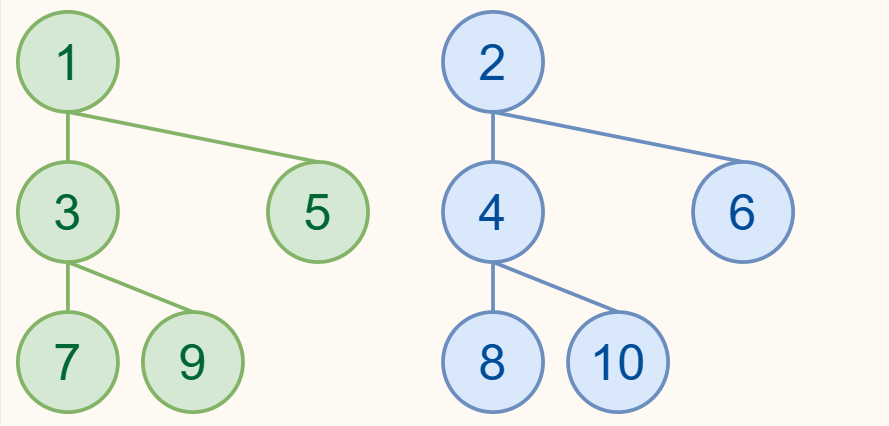
image-20240319165557796

同样从这张图开始，由于我们之前提到的，它类似于一个递归排序的后半部分，具体来说是指合并两个有序数列的过程。

也就是说，我们可以将这两个左偏堆改写成两个有序数列！

image-20240319165605335

由于我们在合并过程中总是找右孩子，所以我们就沿着最右沿路径把没个左偏堆拆成这种“悬吊”的带状形式，每一“条”的值取决于根的键值，也就是这一“条”的最顶部。

在这张图中，我们得到的两个有序数组分别是 [1, 5] 和 [2, 6]，接下来我们将它们进行排序。

image-20240319165612496

经过排序，就会发现它们刚好符合我们在上面步骤得到的结果（可以对比着上面的 Frame 4 看）。实际上，只要你回顾一下归并排序的过程，再对比着看上面的过程，就会发现一模一样。

4.1.3 单点插入

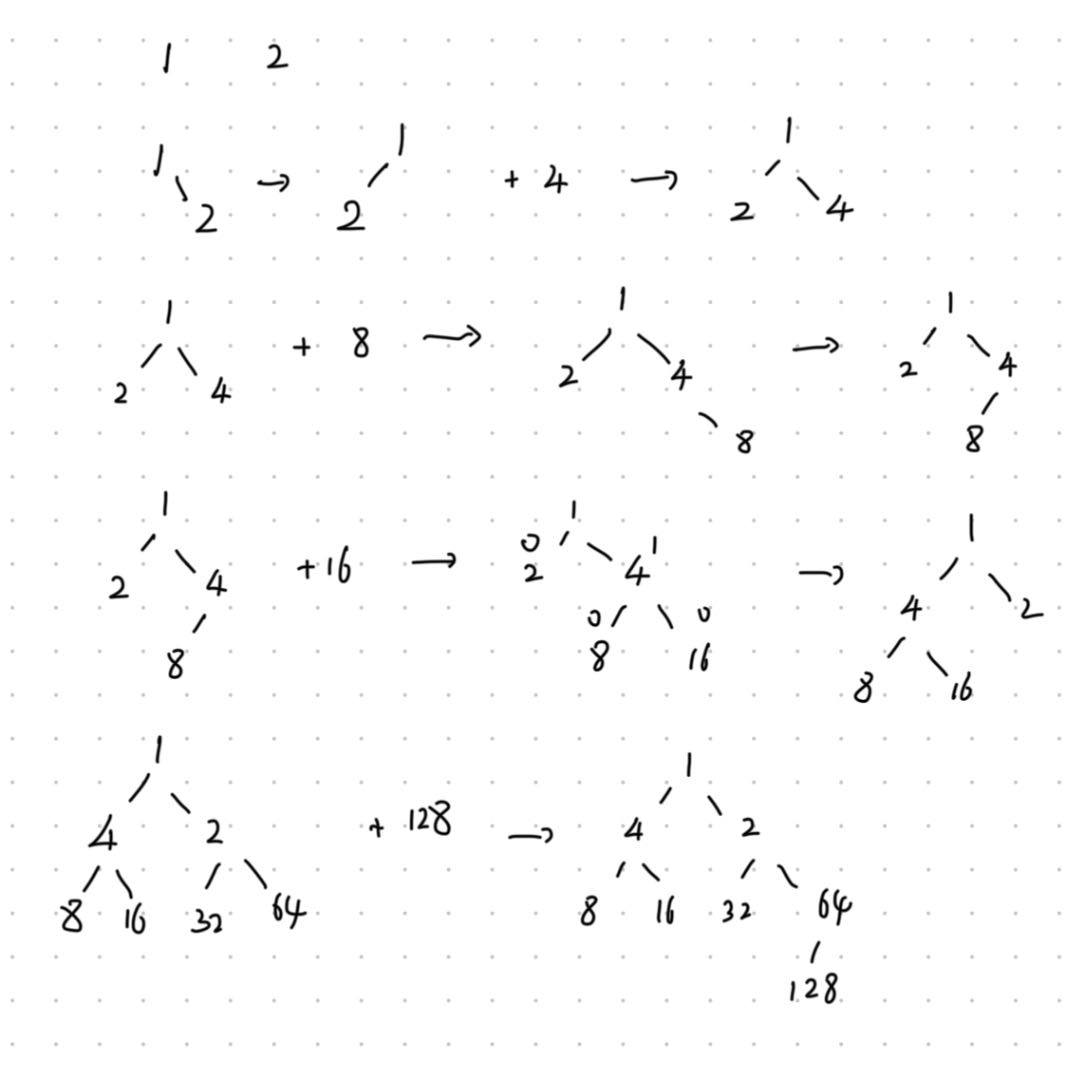
插入结点可以看作合并一个只有一个结点的左偏堆，所以我们可以直接复用合并过程。

PriorityQueue Insert(int x, PriorityQueue H)
{
    PriorityQueue temp = (PriorityQueue)malloc(sizeof(TreeNode));
    temp->value = x;
    temp->Left = temp->Right = NULL;
    temp->Npl = 0;
    H = Merge_Recursive(temp, H);
    LevelOrder(H);
    return H;
}

4.1.4 单点删除

只需要合并需要被删除的结点的两个子结点，然后将这个新的树的根代替被删除的结点，再在回溯的过程中 bottom-up 地更新 Npl 即可。

PriorityQueue Deletemin(PriorityQueue H)
{
    if (IsEmpty(H))
    {
        printf("Error! Priority Queue is empty!");
        return H;
    }
    PriorityQueue LeftHeap = H->Left;
    PriorityQueue RightHeap = H->Right;
    free(H);
    return Merge_Recursive(LeftHeap, RightHeap);
}

4.2 Skew Heap

斜堆(Skew Heap)是比左偏堆更为一般的数据结构，它同样有着能够快速合并的性质。

斜堆与左倾堆的关系就像是splay tree 与 AVL tree 的关系。splay tree 不再维护AVL tree的bf属性，只需要在访问一个结点之后就无脑地利用zig/zig-zig/zig-zag翻转到根结点

斜堆则是不再维护Npl，也就是说在递归过程中左式堆所有维护结构性质以及更新Npl的操作不再需要。取而代之的是以下操作

  1. 在base case 处理H与NULL连接的情况时，左倾堆直接返回H。但是斜堆必须看H的右路径，我们要求H右路径上除最大结点后都必须交换其左右孩子。
  2. 在非base case时，若 H1的根结点小于H2，如果是左倾堆，我们合并H1的右子树和H2作为H1新的右子树，最后判断这样是否违反性质Npl来决定是否交换孩子。而斜堆则是无脑交换，也就是说每次这种情况，都把H1的左孩子换到右孩子，然后把新合并的插入到H1的左子树上。

​ image-20240319195903707

image-20240421130822125

SkewHeap Merge(SkewHeap H1, SkewHeap H2)
{
    // 当一者为NULL结点时，不进行交换孩子，直接返回，对应路径的最大值
    if(H1 == NULL)
        return H2;
    if(H2 == NULL)
        return H1;
    if(H1->value < H2->value)
    {
        H1->Right = Merge(H1->Right, H2);
        // Mer
        SkewHeap temp = H1->Left;
        H1->Left = H1->Right;
        H1->Right = temp;
        return H1;
    }
    else
    {
        H2->Right = Merge(H2->Right, H1);
        SkewHeap temp = H2->Left;
        H2->Left = H2->Right;
        H2->Right = temp;

        return H2;
    }
}

SkewHeap Insert(int x, SkewHeap H)
{
    SkewHeap SingleNode = Initialize(x);
    SkewHeap temp = Merge(SingleNode, H);
    LevelOrder(temp);
    return temp;
}

4.2.1 合理性分析

以每次只插入一个点为例子说明问题。

进一步对递归旋转到左侧做解释，递归性地转到左侧，使得本来最右侧的路径变到最左侧，即使之后交换会重新访问到这个子树，但此时除了根，其他部分依然是最左侧的路径，也不会再轻易地访问到这次路径。

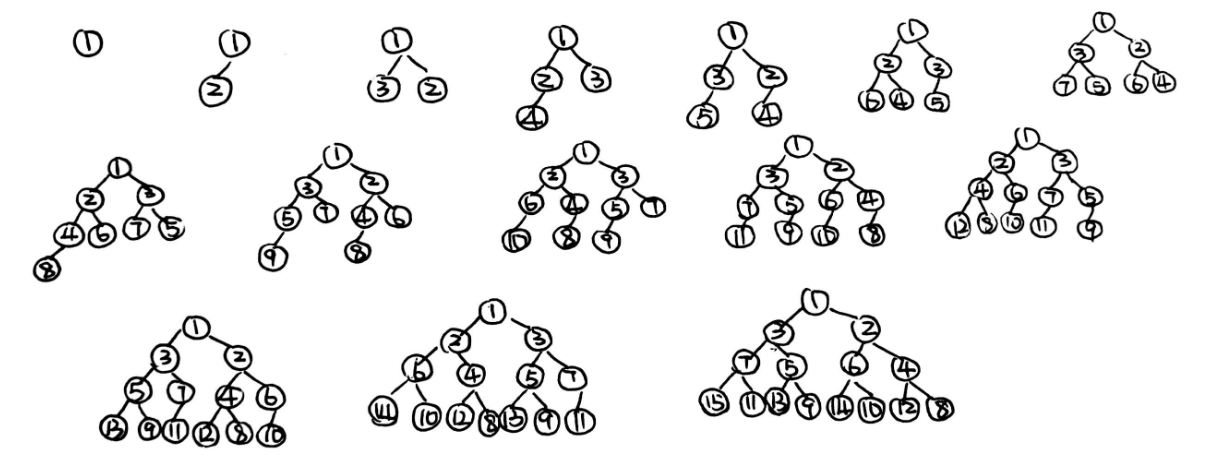
讨论2：判断以下两个说法是否正确，若正确，请给出详细的证明；若不正确，请举出反例： 1. 按顺序将含有键值1, 2, · · · , 2k − 1 的结点从小到大依次插入左式堆，那么结果将形成一棵完全平衡的二叉树。

image-20240319202031988

  1. 按顺序将含有键值1, 2, · · · , 2k − 1 的结点从小到大依次插入斜堆，那么结果将形成一棵完全平衡的二叉树。

4.2.2 摊还分析

势能分析方法回顾

\(D_i\):表示执行第\(i\)遍之后的数据结构

\(c_i\):表示从\(D_{i-1}\)到\(D_i\)的实际成本

\(\hat c_i\):表示从\(D_{i-1}\)到\(D_i\)的均摊成本，\(\hat c_i = c_i + \Phi(D_i) - \Phi(D_{i-1})\)

总均摊成本为：\(\sum \hat c_i = \sum c_i + \Phi(D_n) - \Phi(D_0)\)

分析 skew heap 的均摊复杂度，主要就是分析合并操作的复杂度，因为其他操作都可以转化为合并操作。

引理：对于右路径上有\(l\)个轻结点的斜堆，整个斜堆至少有\(2^l - 1\)个结点，这意味着一个n结点的斜堆右路径上的轻结点个数为\(O(log \ n)\)

证明：

​ 1. 对$ l = 1$显然成立

​ 2. 假设对小于等于\(l\)都成立。对于\(l+1\)情况，我们找到右路径上的第二个轻结点，以它为根节点的子树至少有\(2^l -1\)个结点。 现在考虑第一个轻结点，根据定义，轻结点的左子树更大，而右路径上的第二个轻结点在右子树中。所以第一个轻结点的左子树至少有\(2^l -1\)个结点。 所以整个堆有\(1 + 2^l -1 + 2^l -1 = 2^{l+1}-1\)个结点

定理：若我们有两个斜堆H1和H2， 它们分别由n1和n2个结点，则合并H1和H2的摊还时间复杂度为O(log n), n = n1 + n2

definition "势能函数"

我们定义 \(\Phi(Heap) = \text{number of heavy node in } Heap\)

其中，额外需要定义 heavy node 和 light node：

definition "heavy node & light node"

对于一个子堆 \(H\)，如果 \(size(H.\text{right_descendant}) \geq \frac{1}{2}size(H)\)，则 \(H\) 是 heavy node，否则是 light node。

A node p is heavy if the number of descendants of p’s right subtree is at least half of the number of descendants of p, and light otherwise. Note that the number of descendants of a node includes the node itself.

令\(H_3\)为合并后的新堆，设\(H_i(i = 1,2)\)的右路径上的轻结点数量为\(l_i\),重结点数量为\(h_i\)

真实的合并操作最坏的时间复杂度为\(\sum c_i = l_1 + l_2 + h_1+h_2\)，所有的操作都在右路径上完成

摊还时间成本为\(\sum \hat c_i = \sum c_i + \Phi(H_3) - \Phi(H_1) - \Phi(H_2)\)

将\(h_i^0\)记为不在右路径上的重结点的数量\(\Phi(H_i) = h_i + h_i^0\)

\[ \left\{ \begin{aligned} c &= l_1 + h_1 + l_2 + h_2 &(1)\\ \Phi(H_{3}) &\leq l_1 + h^0_1 + l_2 + h^0_2 &(2)\\ \Phi(H_1) &= h_1 + h^0_{1} &(3)\\ \Phi(H_2) &= h_2 + h^0_{2} &(4) \end{aligned} \right. \]

性质：

  1. 如果一个节点是 heavy node，并且在其右子树发生了合并（包括翻转），那么它一定变为一个 light node；
  2. 如果一个节点是 light node，并且在其右子树发生了合并（包括翻转），那么它可能变为一个 heavy node；
  3. 合并过程中，如果一个节点的 heavy/light 发生变化，那么它原先一定在堆的最右侧路径上;因为其它结点合并前后子树是完全被复制的，所以不可能改变轻重状态

合并后原本不在右路径上的\(h_i^0\)个重结点仍然是重结点，在右路径上的\(h1 + h2\)个重结点全部变成轻结点，\(l1 + l2\) 个轻结点不一定都变重。

\[ \begin{aligned} \Phi(H_3) &<= h_1^0 +h_2^0 + l_1 + l_2 \\ \\ \sum \hat c_i &= \sum c_i + \Phi(H_3) - \Phi(H_1) -\phi(H_2) \\ & <= l_1 + l_2 +h_1+h_2 + (l_1 + l_2 + h_1^0 + h_2^0) - (h_1 + h_1^0 + h_2 + h_2^0)\\ & = 2(l_1 + l_2) = O(log \ n_1 + log \ n_2) = O(log(n_1 + n_2)) \end{aligned} \]

4.3 习题集

  1. The result of inserting keys 1 to \(2^k -1\) for any \(k>4\) in order into an initially empty skew heap is always a full binary tree.

    image-20240321112455601

    True

    数学归纳法证明，首先对于k=4，满二叉树成立

    对于k=5，左右子树的

  2. The right path of a skew heap can be arbitrarily long.

    True

    相对而言，leftist heap 就不能这么任意了，它受$ logN$ 限制。

  3. A skew heap is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than balanced binary heaps. The worst case time complexities for Merge, Insert, and DeleteMin are all \(O(N)\), while the amorited time complexities for Merge, Insert, and DeleteMin are all \(O(logN)\).

    True

    斜堆执行merge，insert，delete最坏时间复杂度为O（N），均摊时间复杂度为O（logN）

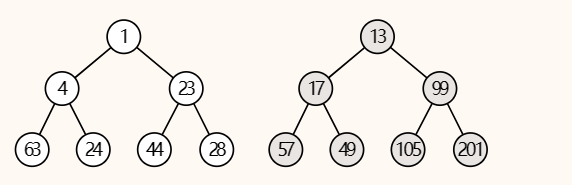
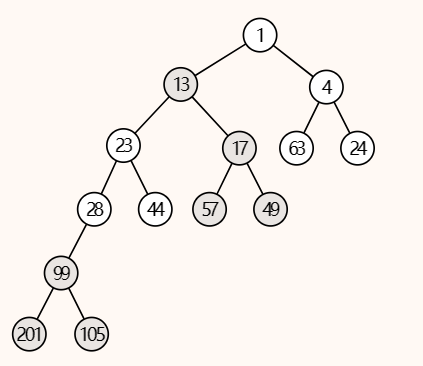
  4. Merge the two leftist heaps in the following figure. Which one of the following statements is FALSE?

    image-20240321113208056

    • A. 2 is the root with 11 being its right child

    • B. the depths of 9 and 12 are the same

    • C. 21 is the deepest node with 11 being its parent

    • D. the null path length of 4 is less than that of 2

      image-20240321113403464

  5. We can perform BuildHeap for leftist heaps by considering each element as a one-node leftist heap, placing all these heaps on a queue, and performing the following step: Until only one heap is on the queue, dequeue two heaps, merge them, and enqueue the result. Which one of the following statements is FALSE?

    • A. in the \(k\)-th run, \(\lceil N/2^k \rceil\) leftist heaps are formed, each contains \(2^k\) nodes

    • B. the worst case is when \(N=2^K\) for some integer \(K\)

    • C. the time complexity \(T(N) = O(\frac{N}{2}log 2^0 + \frac{N}{2^2}log 2^1 + \frac{N}{2^3}log 2^2 + \cdots + \frac{N}{2^K}log 2^{K-1})\) for some integer \(K\) so that \(N=2^K\)

    • D. the worst case time complexity of this algorithm is \(\Theta (NlogN)\)

    C选项得到的时间复杂度为O(N), 与D选项矛盾

    image-20240421134313940

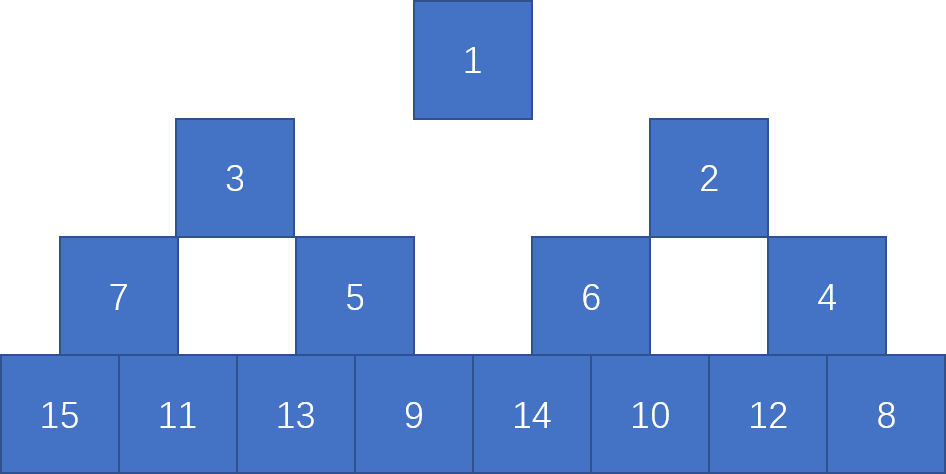
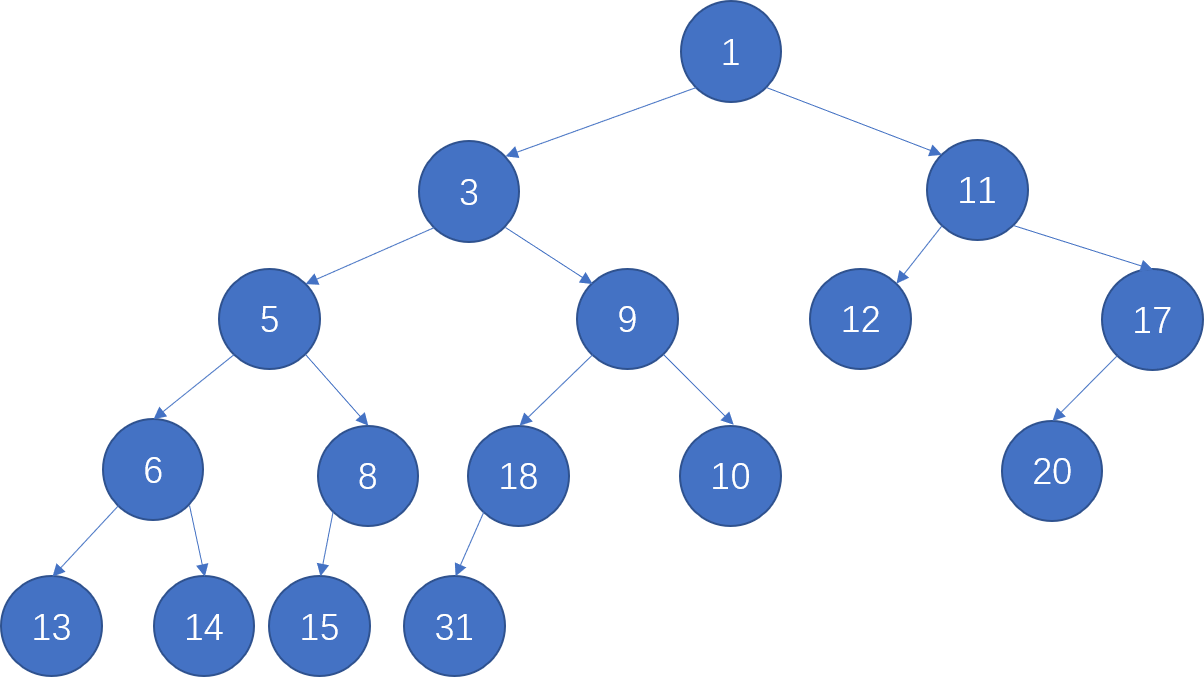
  6. Insert keys 1 to 15 in order into an initially empty skew heap. Which one of the following statements is FALSE?

    • A. the resulting tree is a complete binary tree

    • B. there are 6 leaf nodes

    • C. 6 is the left child of 2

    • D. 11 is the right child of 7

    4.4

    显然，AB选项矛盾，前面得到，结果肯定是满二叉树

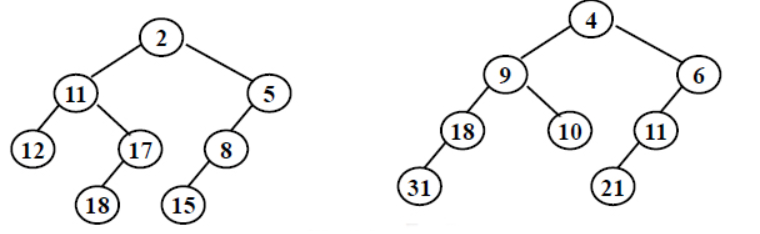
  7. Merge the two skew heaps in the following figure. Which one of the following statements is FALSE?

    • A. 15 is the right child of 8

    • B. 14 is the right child of 6

    • C. 1 is the root

    • D. 9 is the right child of 3

    4.5

    具体思路为：先对右路径结点进行大小排序，分别为1，3，5，6，13

    对应结点的左子树直接移动到右子树即可